Khi nhạc sĩ Saxophone bị bắt thổi nồng độ cồn !!!

Xem cấm cười !

GIẢI TRÍ VỚI BÀI TOÁN CHIA ĐẤT

| Phiên bản dự toán 2023 trở về thuế VAT 10% | Tra mã hiệu dự toán theo tên c/việc |

Một bạn ở huyện Sơn Hòa vừa gửi tôi 1 bài toán rất thực tế như sau:

Người hàng xóm của bạn ấy cần chia đôi miếng đất hình thang ABCD, thành 2 phần cho 2 người con, bằng 1 đường thẳng, điều kiện: 2 phần có diện tích bằng nhau (S1=S2) và bề rộng mặt tiền bằng nhau (MA=MD), (cạnh AD tiếp giáp mặt đường, đường phân chia phải đi qua trung điểm M của cạnh AD).

Giải pháp nào cho người hàng xóm của bạn ấy?

* * *

Tuy đây chỉ là dạng toán hình học phẳng (lớp 8), đơn thuần là hình học, không có ẩn số hay lũy thừa gì phức tạp... nhìn đơn giản nhưng cũng khá là hại não cho một giải pháp.

Bài toán chia đất có tính ứng dụng cao trong thực tiễn, giải pháp đã có, tuy nhiên yêu cầu vẫn được đưa lên để anh em tham khảo, giải trí cho vui.

Hình mang tính gợi ý:

Cách 1:

Thử kiểm tra với trường hợp ngẫu nhiên: BC//AD:

Khi đó C = B' = C', => O là trung điểm BB' (đúng)

Cách 2:

Thử kiểm tra với trường hợp ngẫu nhiên: BC//AD:

Khi đó BC = AD, AB = CD, thay vào công thức trên: 

OH = AD.CD/(CD+AB) = BC.CD/2CD = BC/2, => O là trung điểm BC' (đúng).

* * *

Tuy Hòa, 01/02/2023, Tuấn Anh

* * *

Phản hồi từ Sơn Hòa:

OK anh sau khi em vẽ lại theo cả 2 cách trên và đo diện tích trên AutoCAD thì thấy đúng là 2 phần bằng nhau. Nhưng ổng nói ổng còn 1 miếng đất nữa cũng muốn chia như vậy nhưng miếng này 2 cạnh đối không song song nhau (hình tứ giác lồi chứ không phải hình thang). Vậy cách chia trường hợp này sao anh?

* * *

Với trường hợp này vẫn chia như cách 1 ở trên, xem hình minh họa cách chia (cách 1):

Trường hợp đỉnh B gần cạnh AD hơn:

Thử kiểm tra với trường hợp ngẫu nhiên: BC//AD: 

Khi đó C = B' = C', => O là trung điểm BB' (đúng).

Tưởng xong mà vẫn chưa…

Phản hồi từ Sơn Hòa (15/2/2023):

Anh, cho em xin số tài khoản, ông bạn có ý chuyển anh ít đồng café thay lời cảm ơn vì anh đã giúp đỡ, ổng ở xa ko xuống được.

Và cũng nhân tiện nhờ anh cho 1 phương án dự phòng cuối cùng, đó là thay vì chia làm 2 như trên, thì giờ chia làm 3 như hình dưới (vẫn miếng đất hình tứ giác lồi tiếp giáp mặt đường, chia 3 phần có diện tích bằng nhau, và bề rộng mặt tiền bằng nhau):

Tiêu đề bài viết nên đổi từ "Giải trí..." thành "Hại não..." có lẽ phù hợp hơn, thật may cuối cùng cũng đã tìm ra ánh sáng cuối đường hầm:

* Nhận xét:

Việc chia 3 sẽ không áp dụng theo 1 trong 2 cách trên được, vì việc kẻ đường song song với canh đáy như trên không tạo ra các tam giác bằng nhau để làm "thừa số chung", bài toán lâm vào bế tắc..

Bài toán qui về việc xác định vị trí G, F trên HE, (tức là xác định 3 giá trị x, y, x). xem (x, y, z) là 3 ẩn số, lập 1 hệ 3 phương trình 3 ẩn x, y, z, theo các giá trị đã biết, từ đó tính ra x, y, z (tức xác định được vị trí G, F trên HE)

* Cách xác định G, F:

Giả sử đã xác định được các vị trí các điểm G, F thuộc HE, sao cho BG và CF chia hình tứ giác ADEH thành 3 phần bằng nhau như hình dưới:

Đặt HG = x, GF = y, FE = x.

Cần lập hệ 3 phương trình 3 ẩn số x, y, z, tính được x, y, z là xác định được vị trí G, F trên HE.

Từ A, B, C, D kẻ những đường vuông góc AA’, BB’, CC’, DD’ với cạnh HE, chúng chính là các đường cao tương ứng của các tam giác AHG, BGH, CGF, DFE.

Đặt AA’ = a, BB’ = b, CC’ = c, DD’ = d.

Nối GA, GC, FA, FD.

Nhận thấy: S(GAB) = S(GBC), vì 2 tam giác có chung chiều cao và cạnh đáy bằng nhau. Tương tự: S(FBC) = S(FCD).

Theo yêu cầu: S(ABGH) = S(BCFG)   (*)

Mà:  S(ABGH) = S(GAB) + S(AGH)   (a)

        S(BCFG) = S(GBC) + S(CFG)   (b), thay (a) và (b) vào (*) được:

S(GAB) + S(AGH) = S(GBC) + S(CFG)  <=> S(AGH) = S(CFG)

<=> AA’.HG = CC’.FG <=> a.x = c.y  (với: a khác 0, vì H <> A)

<=> x = (c/a).y (1)

Tương tự ta cũng có: S(BGF) = S(DEF) <=> y = (d/b).y (2)

Đặt FE = m (m là đơn vị chiều dài), => x+y+z = m (3)

Cuối cùng ta có hệ phương trình:

x = (c/a).y (1)

y = (d/b).z (2)

x+y+z = m (3)

Đặt k1 = c/a, k2 = d/b, hệ phương trình trên thành:

x = k1.y (1)

y =  k2.z (2)

x+y+z = m (3)

Với k1, k2 đã biết, m đã biết từ số liệu đo đạc

Giải hệ phương trình trên bằng cách qui về 1 biến:

Từ (2) => z = y/k2, thay vào (3): k1.y + y + y/k2 = m

<=> y(k1+1+1/k2) = m <=> y = m/(k1+1+1/k2)

Đến đây tính được y, thay vào (1) tính được x, thay vào (2) hoặc (3) tính được z.

Giá trị x, y, z chính là độ dài HG, GF, FE. Từ đó xác định được vị trí các điểm G, F trên HE.

Bài toán xem như được giải quyết.

* Kiểm tra với các trường hợp đặc biệt:

1. H trùng A:

Khi đó hình tứ giác ADEH trở thành tam giác ADE, và x=y=z=m=0

<=> G, F, trùng E. => 3 phần diện tích là 3 tam giác EAB, EBC, ECD, có các cạnh đáy bằng nhau, chung chiều cao hạ từ E nên chúng bằng diện tích: thỏa mãn yêu cầu đặt ra.

2. Cạnh HE//AD:

Khi đó: a=b=c=d => k1 = c/a = 1, k2 = d/b = 1.

=> x=y=z, <=> HG=GF=FE

=> 3 phần diện tích là 3 hình thang ABGH, BCFG, CDEF, có các cặp cạnh đáy // và bằng nhau từng đôi một và có chiều cao bằng nhau (do 2 đáy //), nên chúng bằng diện tích: thỏa mãn yêu cầu đặt ra.

Có thể kiểm tra kết quả bằng phần mềm AutoCAD hoặc trên thực địa: Để kiểm tra trên thực địa ta cần nhớ lại cách tính diện tích hình tứ giác lồi: Nối 2 đỉnh đối diện của tứ giác bằng 1 đường chéo, đường này chia tứ giác thành 2 tam giác chung cạnh đáy là đường chéo đó, từ 2 đỉnh còn lại hạ 2 đường cao xuống đường chéo, từ đó tính được diện tích 2 tam giác, diện tích tứ giác bằng tổng diện tích 2 tam giác, từ đó tính được S, S1, S2, S3. Kiểm tra: S= S1+S2+S3.

* Tổng kết:

Phương pháp chia 3 ở trên có thể áp dụng cho các trường hợp chia hình tứ giác thành n  phần bằng nhau (n là số nguyên >= 2 (2, 3, 4, 5...)), và có bề rộng cạnh chung bằng nhau. Khi đó số biến (x, y... sẽ bằng số phần cần chia n).

- Nếu miếng đất hình thang (2 cạnh bên //) và chia 2 phần: Áp dụng 1 trong 2 cách trên cùng, trong đó cách 1 đơn giản hơn một chút;

- Nếu miếng đất hình tứ giác và chia 2 phần: Áp dụng cách 1 (xem hình minh họa ở trên);

- Nếu chia 3 phần thì áp dụng cách dưới cùng, phương pháp chia 3 vẫn có thể áp dụng cho cả trường hợp chia 2.

Cuối cùng, các yêu cầu của bạn ấy cũng đã được giải quyết.

| Giải trí với vài đường bida 3 băng |

THƠ VUI NGÀY TẾT...

| Giải trí với bài toán chia đất |

Sáng mùng 1 tết 2023, cafe một mình tại nhà, và sau đây là thành quả...

Bổ sung năm trước:

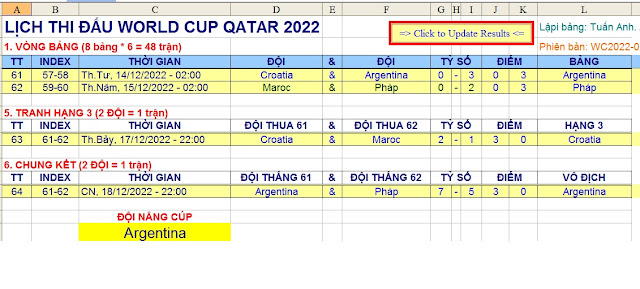
File excel tự động cập nhật kết quả World Cup QATAR 2022 - The excel file auto updates the results of the World Cup QATAR 2022

File excel tự động cập nhật kết quả World Cup QATAR 2022

The excel file automatically updates the results of the World Cup QATAR 2022

* Lưu ý:

+ File chỉ hoạt động trên máy tính, không hoạt động trên điện thoại.

+ Kích hoạt macro excel trước khi sử dụng.

* Công dụng:

- Theo dõi lịch thi đấu;

- Tự động cập nhật kết quả bằng cách Click chuột 1 cái…

- Xếp hạng các đội từ vòng bảng đến chung kết;

- Tham khảo công thức excel vận dụng vào việc khác.

* Tác giả: Tuấn Anh. Zalo: 0919410280. Ngày lập: 21/11/2022.

(File được làm theo đơn đặt hàng và được sự đồng ý chia sẻ)

* Link tải file excel lịc thí đấu WorldCup 2022 và tự động cập nhật:

Tải về để sử dụng trên máy tính: TẠI ĐÂY

Link trên đã update bản sửa lỗi (25/11/2022), nhầm lịch thi đấu vòng 1/8.

* * *

Kết quả giải đấu (19/12/2022):

Người xưa từng nói: “Đường xa mới biết ngựa hay”.

* Argentina lách mình qua khe cửa hẹp sau trận thua sấp mặt Saudi Arabia ở vòng bảng, để rồi sau đó băng băng tiến thẳng vào tận trận chung kết và hạ bệ luôn đương kim vô địch Pháp để cướp ngôi. => Khởi đầu không tốt chưa phải là thất bại. Thất bại chỉ thực sự đến khi mất niềm tin và chiến thắng vẫn đến nếu đủ độ “lì đòn”, không bao giờ bỏ cuộc.

* Saudi Arabia gấy chấn động thế giới với chiến thắng tưng bừng trước cựu vô địch thế giới Argentina ở vòng bảng, để rồi sau đó bị loại cũng ở ngay vòng bảng. => Phong độ chỉ nhất thời. Khởi đầu tốt chưa đủ để có kết quả tốt nếu chưa đủ “đẳng” và độ “lì đòn”, hoặc chủ quan, ngủ quên trong chiến thắng. 

| Thế nào để làm được 1 video karaoke giải trí, kỷ niệm… ? |

NHỮNG ĐƯỜNG CONG ĐẸP TRONG KIẾN TRUC

Xem thêm:

| Dự toán Phú Yên 2021 cập nhật định mức thông tư 11, 12/TT-BXD |

| TRA MÃ HIỆU DỰ TOÁN THEO TÊN CÔNG VIỆC |

| Tấu hài cực mạnh: “Vậy là cuối cùng họ cũng phá được con đường tốt nhất” |

* * *

Thảo luận, chia sẻ chút kinh nghiệm nhỏ với anh em xây dựng:

Nếu trong bi-da có những đường cơ đẹp thì trong kiến trúc cũng có những đường cong đẹp.

Hôm trước có anh em e-mail trao đổi 1 vấn đề: Tôi làm thầu xây dựng, thỉnh thoảng có gặp mấy nhà dân thiết kế cửa vòm, anh em ký thuật và thợ vẫn lúng túng khi tạo vòm, có khi làm xong chủ nhà, hay thiết kế nói vòm chưa đẹp, chưa đạt yêu cầu, họ nói do thợ tạo vòm theo cảm tính, sai ý thiết kế… yêu cầu làm lại, vậy có đúng là tôi đã làm sai không ? căn cứ vào đâu để khẳng định sai-đúng ? và làm lại thì làm thế nào cho đúng ? Có “công thức chung” nào cho các loại vòm này không nhỉ ?

* * *

Đường cong thường được sử dụng trong các công trình kiến trúc

Dạo này dịch dã (2021) cho nên thời gian café, lai rai quán xá, bi-da hay live-show ca nhạc… không còn nhưng lại có thời gian để quay trở lại trao đổi với anh em xây dựng, nhà thầu về chủ đề này, chỉ là chút kinh nghiệm nhỏ, vì trước đây tôi cũng vài lần gặp các trường hợp tương tự. Có gì chưa ổn mong anh em KTS bỏ quá và lượng thứ.

Mới nghe nghĩ cũng đơn giản nhưng sự thật sự không đơn giản với ai chưa có kinh nghiệm, vì vấn đề này có liên quan đến kiến thức hình học phẳng thời phỏ thông, mà anh em kỹ thuật lăn lộn công trường lâu ngày có khi cũng mai một ít nhiều.

Ngoài đường thẳng thì đường cong cũng rất thường được sử dụng trong các công trình kiến trúc, cầu cống, về mặt thẩm mý, nó mang nét mềm mại, đẹp mắt, về mặt kết cấu, nó tạo cảm giác cân xứng, vững chắc, an tâm.

Ta thường bắt gặp các còm này trên các khung cửa, vòm cầu… ở đây tôi chỉ trao đổi một kinh nghiệm thực tế là cách dựng 1 vòm cong trên khung cửa công trình xây dựng dân dụng, sao cho đúng kích thước, đúng quĩ đạo, từ đó tạo cảm giác mềm mại, đẹp mắt.

Có thể chia ra một số kiểu vòm thường gặp:

1. Vòm có dạng 1 cung tròn, giao cắt với 2 cạnh đứng 2 bên khung cửa tại 2 điểm mút:

- Mô tả: Như hình dưới, đường màu đỏ là vòm cần dựng. 

- Tính toán và dựng hình:

Gọi 2 đỉnh góc trái, phải của cửa là A, B. O là trung điểm AB, OH là chiều cao vòm, => 3 điểm A, B và H đã biết và nằm trên 1 cung tròn, giờ cần xác định tâm của cung tròn đó.

Cung tròn đó là 1 đoạn của đường tròn tâm O₁ => AO₁ = BO₁ => O nằm trên đường thẳng đứng đi qua trung điểm O của AB.

Lại vì HO₁ = BO₁ => O₁ cách đều B, H => O₁ nằm trên trung trực BH.

Xác định tâm O₁

Từ trung điểm O của AB dựng đường thẳng _|_ AB, từ trung điểm của BH dựng 1 đường thẳng khác _|_ BH, giao của 2 đưởng thẳng này chính là O₁.

Từ O₁ vẽ vòng tròn có bán kính AO₁, vòng tròn này sẽ đi qua A, H, B.

Cung AHB là vòm cửa cần dựng.

Chiều cao x (=OH) của vòm thường trong khoảng: (1/6)AB < x < (1/2)AB

Trường hợp đặc biệt: x = AO₁-AA₁ <=> OH = HO₁-AA₁ (1)

Mà OH = HO₁-OO₁ (2)

(1)&(2)=> OO₁ = AA1 => tâm cung tròn là trung điểm A₁B₁

Đây là trường hợp thường áp dụng vì dễ thi công.

2. Vòm có dạng 1/2 Ellipse (E-lip), không có giao cắt với 2 cạnh đứng 2 bên khung cửa tại 2 điểm mút, mà chỉ tiếp xúc (góc giữa vòm và 2 cạnh đứng tại 2 điểm mút = 0):

- Mô tả: Như hình dưới, đường màu đỏ là vòm cần dựng.

- Tính toán và dựng hình:

Ở dạng 1, cung AHB là 1 cung tròn, tâm là 1 điểm.

Dạng 2 này cung AHB là ½ Ellipse trục ngang AB. Trục đứng OH. Và vì nó có dạng Ellipse nên cần xác định 2 tâm điểm F₁. F₂ của Ellipse (hình Ellipse có 2 tâm nằm trên trục lớn), với 3 điểm A, B và H đã biết.

Nhớ lại kiến thức phổ thông:

Ở toán 10 chỉ nêu công thức xác định vị trí F₁. F₂ theo A, A₁, B, B₁ (c² = a² - b²) mà không ch/minh (chứng minh như trên hình).

Như vậy có OA = c, OH = b, tính ra được c = OF₁, OF₂, từ đó xác định được vị trí F₁. F₂.

Một cách khác đơn giản hơn, dễ áp dựng vào thực tế thi công hơn:

Vì HF₁ + HF₂ = AB => HF₁ = OA => dựng hình tròn tâm H, bán kính r = OA, cắt AB tại 2 điểm F₁, F₂ là 2 tâm điểm Ellipse.

Xác định được F₁, F₂ theo các điểm A, B, H, giờ dựng Ellipse:

Đóng đinh hay cách nào đó để cố định các điểm F₁, F₂, H.

Dùng 1 sợi dây không co dãn, 2 đầu buộc cố định vào F₁, F₂, và móc qua điểm H (HF₁ + HF₂ = AB).

Dùng bút chỉ đặt tại điểm A, nằm bên trong sợi dây, kéo lên lên và qua phải, từ A đến H, B ta được cung AHB. Cung AHB là vòm cửa cần dựng.

Chiều cao x (=OH) thường trong khoảng: (1/6)AB < x < (1/2)AB

Trường hợp đặc biệt: x = (½)AB, khi đó F₁=F₂=O, cung tròn = ½ vòng tròn đường kính AB.

3. Vòm có dạng kết hợp vòng tròn và đoạn thẳng:

4. Vòm có dạng kết hợp vòng tròn và cung Ellipse hoặc cung tròn:

Hai dạng dạng vòm 1&2 là dạng vòm đơn (chỉ 1 loại cung tròn); vòm 3&4 là dạng vòm kết hợp [vòng tròn + đoạn thẳng] và [vòng tròn + cung Ellipse hoặc cung tròn], anh em tự tìm hiểu thêm.

* * *

Ellipse là một đường cong rất đẹp nếu thi công đúng quĩ đạo của nó

Đường tròn, và nhất là đường Ellipse, rất hay được sử dụng trong các công trình kiến trúc, nhất là các công trình kiến trúc cổ của Pháp (có nhiều ở Sài Gòn, Hà Nội, Đà Lạt)

Vấn đề là khi thi công anh em kỹ thuật, kỹ sư xác định sao cho đúng quĩ đạo cong của nó. Nếu không đúng sẽ làm mất đi vẻ đẹp của công trình - và ngược lại:

So sánh bản gốc và bản sao – quĩ đạo cong của bản sao có vẻ như bị "trật bài" 

Ngoài việc xác định quĩ đạo vòm cong thì do tường có chiều dày nên cũng phải kiểm soát bề mặt của bụng vòm (nó phải vuông góc với mặt phẳng tường), có thể dùng Eke 90⁰ (thước góc vuông |_)

Khi được thi công đúng quĩ đạo, những cung tròn sẽ đều như đúc và rất đẹp mắt:

* * *

MỘT SỐ CÔNG TRÌNH KẾN TRÚC VỚI CÁC ĐƯỜNG CONG ĐẸP MẮT:

- Bưu điện Sài Gòn - điểm đến thu hút khách du lịch quốc tế:

- Tòa thị chính Sài Gòn xưa – nay là UBND TP HCM - di tích kiến trúc nghệ thuật:

- Một trường học với kiến trúc Pháp:

- Bên trong một giáo đường với kiến trúc Pháp:

- Một số hình ảnh khác:

* * *

TP Tuy Hòa 05/9/2021 - Ng.T.Anh

NHỮNG TRÒ "MA MỊ" TRONG THỂ THAO, GIẢI TRÍ

[ Chuyên mục: Giải trí ]

1. Bạch tuộc dự đoán đá banh World cup

Luôn yêu thích bên phải

Bạch tuộc Paul đã đoán "trúng phóc" 6 trận banh World cup 2010, nhưng có thật là nó biết trước được tương lai ?

Sự thật là bạch tuộc luôn yêu thích những chiếc hộp ở bên phải. Trong số 6 lần "phán", Paul chỉ duy nhất 1 lần mở nắp chiếc hộp ở bên trái. Đó là trận đấu giữa Anh và Đức tại vòng 1/8. 5 trận đấu còn lại, những chiếc hộp yêu thích của Paul lại luôn nằm ở bên phải.

Trong buổi tường thuật trực tiếp lễ "đăng đàn" của Paul, các nhân viên (không hiểu vô tình hay cố ý) đã luôn để chiếc hộp có quốc kì của đội được dự đoán trước sẽ thắng ở bên phải, hộp kia ở bên trái. Ngay khi hai chiếc hộp được thả xuống, "thánh" đã ngay lập tức lao thẳng đến chiếc hộp bên phải mà không một chút để ý chiếc hộp bên trái có quốc kì của nước nào.

Nghi ngờ ở đây: Có thể bên phải là hướng yêu thích của Paul

=> Kết luận: Vấn đề là người ta sẽ đặt bên phải cái hộp dán quốc kỳ nước nào mà họ dự đoán sẽ thắng chứ ko phải là con bạch tuộc

Chẳng có yếu tố thần bí hay xác xuất thống kê trong toán học gì ở đây cả, chỉ là một mẹo mà người tổ chức đã dự đoán trước đội thắng, sau đó bỏ cái hộp có quốc kỳ của đội dự đoán sẽ thắng ở bên phải, để rồi theo một thói quen vô thức, con bạch tuộc sẽ đi đến cái hôp bên phải đó. Khi may mắn xảy ra, mọi người sẽ lầm tưởng là nó có tài dự đoán.

Vì thực chất một con vật nó sao hiểu đá banh là gì mà dự đoán, hơn nữa nó cũng đâu biết quốc kỳ là của đội nào, đem thay 2 quốc kỳ bằng 2 miếng vải bất kỳ, thậm chí bỏ hẳn quốc kỳ, thì nó cũng thì nó cũng vẫn bò sang phải thôi.

Vậy nhưng nhiều người không hiểu được nguyên nhân nên rất ca ngợi con vậy này: "Bạch tuộc  Paul rất thông minh. Trí thông minh của chúng có thể sánh ngang với những chú chó nhạy bén nhất…"

Hết bạch tuộc, người ta còn nghĩ ra đủ trò như mèo, lạc đà, lơn… với nhiều mụch đích khác nhau.

2. Mèo tiên tri dự đoán sai bét kết quả Euro 2020

Đúng 10 – sai 13 trận

Tương tự bạch tuộc, con mèo gì đó dự đoán kết quả Euro 2020 cho kết quả sai bét: đa số mèo đi sang bên phải theo thói quen mà không cần biết bên kia (hoặc ở giữa) là gì:

* * *

3. Chó làm toán

Trò sau đây cũng là 1 trò tương tự: Hồi nhỏ chắc mọi người cũng có thể đã đi xem xiếc thú, khi lái xe, chó làm toán…. Trong đó trò “chó làm toán” gây thích thú cho nhiều người, nhất là các bạn nhỏ,

- Khi người biểu diễn (cũng là người “thầy” của chó) hỏi con chó 1 bài tính cộng: 2+3 = mấy ? con chó sủa "gâu", "gâu"… 5 tiếng. Nó được ngay 1 cục xương hay cục gì đó là phần thưởng !

- Tiếp theo, người biểu diễn hỏi con chó bài tính trừ: 6-3 = mấy ? con chó sủa 3 tiếng.

- Tiếp theo, người biểu diễn hỏi con chó bài tính nhân: 2*3 = mấy ? con chó sủa 6 tiếng.

Mọi người ko hiểu sao con vật lại biết làm toán.

Sự thật là gì? Con chó đã được huấn luyện để sủa theo một trong các cách:

1. Sủa 3 lần theo các thứ tự: chuỗi 5, 3, 6 (ví dụ thế), ngày nào nó cũng lập đi lặp lại như vậy đến thuộc lòng theo thứ tự đó. Khi biểu diễn chỉ việc mớm câu hỏi để trùng đáp án là được.

Ví dụ: lượt đầu sẽ là 5 tiếng sủa thì câu hỏi có thể là: 2+3 = ? hay 4+1 = ?

Lượt 2 sẽ là 6 tiếng sủa thì câu hỏi sẽ là: 6*1 = ? Hay 3*2 = ?  Hoặc 3*4-6 =  ?

Một thử nghiệm đã chứng minh: Nếu đặt câu hỏi 1+1 = ? Nó vẫn cứ sủa 5 tiếng.

2. Sủa theo tín hiệu bí mật, tín hiệu có thể bằng âm thanh (đủ to để con chó nghe trên sân khấu, nhưng đủ nhỏ để khán giả bên dưới không nghe), hay một cử chỉ, ám hiệu nào đó mà con chó đã được huấn luyện từ trước). Trường hợp này có thể đặt câu hỏi tùy ý, người biểu diễn khi đó chỉ việc ra tín hiệu để chó sủa theo cho đúng. Khi đã sủa đủ thì tắt tín hiệu để nó không sủa nữa.

=> Vấn đề là con người chứ không phải là con chó.

* * *

Nói chung là trong xã hội từ trước giờ người ta luôn nghĩ ra đủ trò để thu hút sự theo dõi của đám đông vì mục đích giải trí hay tư lợi gì đó, nếu mọi người không nhận ra được cái gì ẩn sau những hiện tượng đó thì sẽ dễ cho đó là những câu chuyện huyền bí, ma mị, và đôi khi mất tiền vì những niềm tin vô căn cứ ấy.

(TuanAnh – t.h.& s.t)